Triad Method
Triad is one of the earliest and simplest solutions to the spacecraft attitude determination problem,.[1][2] As evident from the literature, TRIAD represents the state of practice in spacecraft attitude determination, well before the advent of the Wahba [3] problem and its several optimal solutions. Given the knowledge of two vectors in the reference and body coordinates of a satellite, the TRIAD algorithm obtains the direction cosine matrix relating both frames.
Contents |
Summary
We consider the linearly independent reference vectors 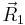 and
and 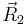 . Let
. Let 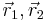 be the corresponding measured directions of the reference unit vectors as resolved in a body fixed frame of reference. Then they are related by the equations,
be the corresponding measured directions of the reference unit vectors as resolved in a body fixed frame of reference. Then they are related by the equations,
-
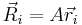
(
for 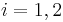 , where
, where  is the proper orthogonal matrix (i.e.,
is the proper orthogonal matrix (i.e., 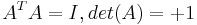 ) that transforms vectors in the body fixed frame into the frame of the reference vectors. Note that the direction cosine matrix
) that transforms vectors in the body fixed frame into the frame of the reference vectors. Note that the direction cosine matrix  also transforms the cross product vector, written as,
also transforms the cross product vector, written as,
-
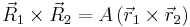
(
Triad proposes an estimate of the direction cosine matrix of interest as a solution to the linear system equations given by
-
![\left[ \vec{R}_1 ~\vdots~ \vec{R}_2 ~\vdots~ \left(\vec{R}_1 \times \vec{R}_2 \right) \right] = A \left[ \vec{r}_1 ~\vdots~ \vec{r}_2 ~\vdots~ \left( \vec{r}_1 \times \vec{r}_2 \right) \right]](/2012-wikipedia_en_all_nopic_01_2012/I/9972d92f0e81783d6a773fbae9b4d76d.png)
(
where  have been used to separate different column vectors.
have been used to separate different column vectors.
The solution presented above works well in the noise-free case. However, in practice,  are noisy and the orthogonality condition of the attitude matrix (or the direction cosine matrix) is not preserved by the above procedure. Triad incorporates the following elegant procedure to redress this problem. To this end, we define unit vectors
are noisy and the orthogonality condition of the attitude matrix (or the direction cosine matrix) is not preserved by the above procedure. Triad incorporates the following elegant procedure to redress this problem. To this end, we define unit vectors
-
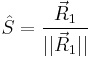
(
-
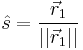
(
and
-
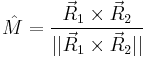
(
-
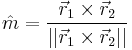
(
to be used in place of the first two columns of (3). Their cross product is used as the third column in the linear system of equations obtaining a proper orthogonal matrix for the spacecraft attitude given by
-
![\left[ \hat{S} ~ \vdots ~ \hat{M} ~\vdots~ \hat{S} \times \hat{M} \right] = A \left[ \hat{s} ~\vdots~ \hat{m} ~\vdots~ \hat{s} \times \hat{m} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/655d5b10ae2acfa4eeb9b4d16e650b24.png)
(
Thus an estimate of the spacecraft attitude is given by the proper orthogonal matrix as
-
![\hat{A} = \left[ \hat{S} ~ \vdots ~ \hat{M} ~\vdots~ \hat{S} \times \hat{M} \right] \left[ \hat{s} ~\vdots~ \hat{m} ~\vdots~ \hat{s} \times \hat{m} \right]^T.](/2012-wikipedia_en_all_nopic_01_2012/I/8e8b120348f26cb6eeb059ff262b9b23.png)
(
Note that computational efficiency has been achieved in this procedure by replacing the matrix inverse with a transpose.
Triad Attitude Matrix and Handed-ness of Measurements
It is of consequence to note that the Triad method always produces a proper orthogonal matrix irrespective of the handedness of the reference and body vectors employed in the estimation process. This can be shown as follows. Let us re-write Eq. (8) in a matrix form given by
-
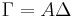
(
where ![\Gamma�:= \left[ \hat{S} ~ \vdots ~ \hat{M} ~\vdots~ \hat{S} \times \hat{M} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/3289fe1e9c4fbed7b6155c4daaa52e1d.png) and
and ![\Delta = \left[ \hat{s} ~\vdots~ \hat{m} ~\vdots~ \hat{s} \times \hat{m} \right].](/2012-wikipedia_en_all_nopic_01_2012/I/04fd02230259ca6c2e763f026bd86651.png) Note that if the columns of
Note that if the columns of  form a left handed triad, then the columns of
form a left handed triad, then the columns of  are also left handed because of the one-one correspondence between the vectors. This is because of the simple fact that, in Euclidean geometry, the angle between any two vectors remains invariant to coordinate transformations. Therefore, the determinant
are also left handed because of the one-one correspondence between the vectors. This is because of the simple fact that, in Euclidean geometry, the angle between any two vectors remains invariant to coordinate transformations. Therefore, the determinant 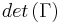 is
is 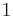 or
or 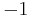 depending on whether its columns are right or left - handed respectively (similarly,
depending on whether its columns are right or left - handed respectively (similarly, 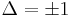 ). Taking determinant on both sides of the relation in Eq. (10), we conclude that
). Taking determinant on both sides of the relation in Eq. (10), we conclude that
-
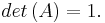
(
This is quite useful in practical applications since the analyst is always guaranteed a proper orthogonal matrix irrespective of the nature of the reference and measured vector quantities.
Applications
Triad was used as an attitude determination technique on-board the Transit system (used by the U.S. Navy for navigation). It is interesting to note that the principles of the Transit system gave rise to what we now know as the GPS satellite constellation. In an application problem, the reference vectors are usually known directions (e.g., stars, Earth magnetic field, gravity vector, etc.). Body fixed vectors are the measured directions as observed by an on-board sensor (e.g., star tracker, magnetometer, etc.). With advances in micro-electronics, attitude determination algorithms such as Triad have found their place in a variety of devices (e.g., smart phones, cars, tablets, UAVs etc.) with a broad impact on the modern society.
See also
References
- ^ Black, Harold (July 1964). "A Passive System for Determining the Attitude of a Satellite". AIAA Journal 2 (7): 1350–1351. doi:10.2514/3.2555.
- ^ Black, Harold (July-Aug 1990). "Early Developments of Transit, the Navy Navigation Satellite System". Journal of Guidance, Control and Dynamics 13 (4): 577–585. doi:10.2514/3.25373.
- ^ Wahba, Grace (July 1966). "A Least Squares Estimate of Satellite Attitude, Problem 65.1". SIAM Review: 385–386.